Collective excitation of a trapped Bose-Einstein condensate with spin-orbit coupling

In recent years, an important breakthrough in cold atom physics is the realization of spin-orbit (SO) coupling [1-5]. The SO coupled Bose gases, which has no analog in conventional solid materials which deal with fermionic systems, present rich many-body quantum phases such as stripe phase [6-7] and skyrmion lattices [8]. However, despite of the tremendous attention they have attracted, direct evidences of these exotic phases are still lacking. Here, we would like especially point out that striped phase has recently been directly observed in the experiment [8]. However, instead of the two hyper-spin states, they used atoms trapped in a double well potential to represent the pseudo-spin degrees of freedom, which is not exactly the model we considered in this work. Therefore, the main purpose of the present work is to show that different phases of an SO coupled Bose-Einstein condensate (BEC) features distinctive collective excitations, which can therefore be used to distinguish various phases.

The theoretical model we use here is same with that in Ref.[3], where an effective one-dimension two-component BEC system is coherently coupled by two Raman beams propagating along the x-axis with vanishing two-photon detuning. The static and dynamic behavior at T=0 are govered by a coupled Gross-Pitaevskii equations, based on which we then calculate the Bogoliubov spectrum by numerically solving Bogoliubov equations, and one typical spectrum depending on Raman coupling strength is plotted as follows:

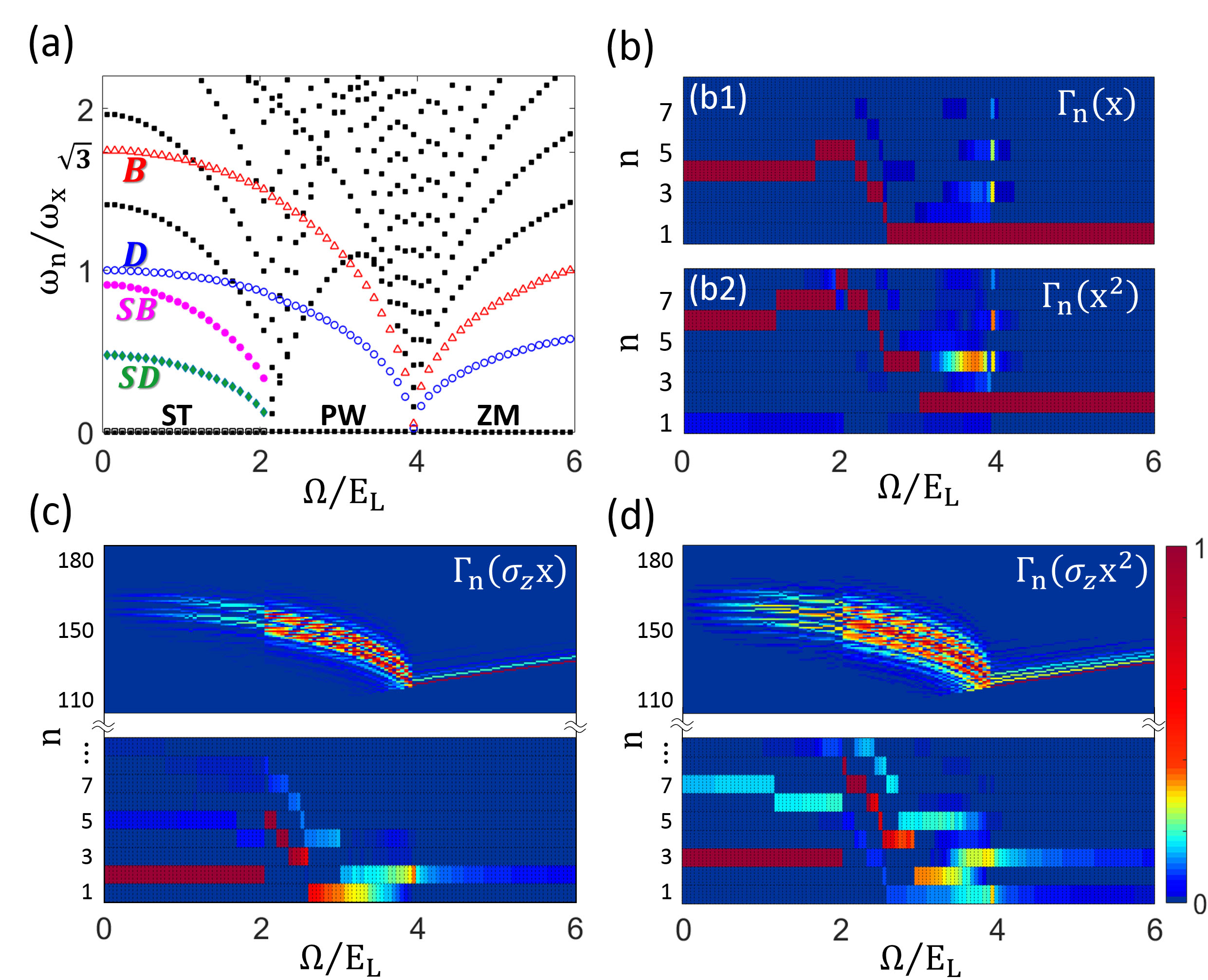
Fig. 1

One can observe that there are two important features in this spectrum: a) In striped phase (ST), there are two lower-lying modes whose frequencies are very close to zero. These two modes will be exactly vanishing in thermodynamic limit corresponding to two Goldstone mode spontaneously breaking U(1) gauge symmetry and translational symmetry simultaneously. b) Spectrum exhibits mode softening near the two critical Raman coupling strength where the system changes from one phase to another. In particular, the spin-independent modes, such as dipole and breathing, are soften near the plane-wave (PW)/ zero-momentum (ZM) phase boundary, while the spin-dependent modes, such as spin dipole and spin breathing, are soften near the ST/PW phase boundary.

In our work, we especially discussed the spin-dependent dynamics in a quench process. We observed that distinct features in the three phases when a small spin dipole (breathing) perturbation is added into the system. By calculating the elementary transitional strength (see (b), (c) and (d) in Fig. 1), we can always find a dominant in ST and ZM phase which means the spin dipole mode would nearly oscillate in a sinusoidal way (see Fig. 2(b) and (d)). However, in PW phase, a finite perturbation is able to change the BEC from a miscible to an immiscible condition. Such a huge change of the static response to the spin dipole perturbation will finally leads to a complete nonlinear but non-trivial dynamic oscillation as shown in Fig. 2(c). We hope that our work may stimulate more experimental study of the collective excitation properties of SO coupled BEC.

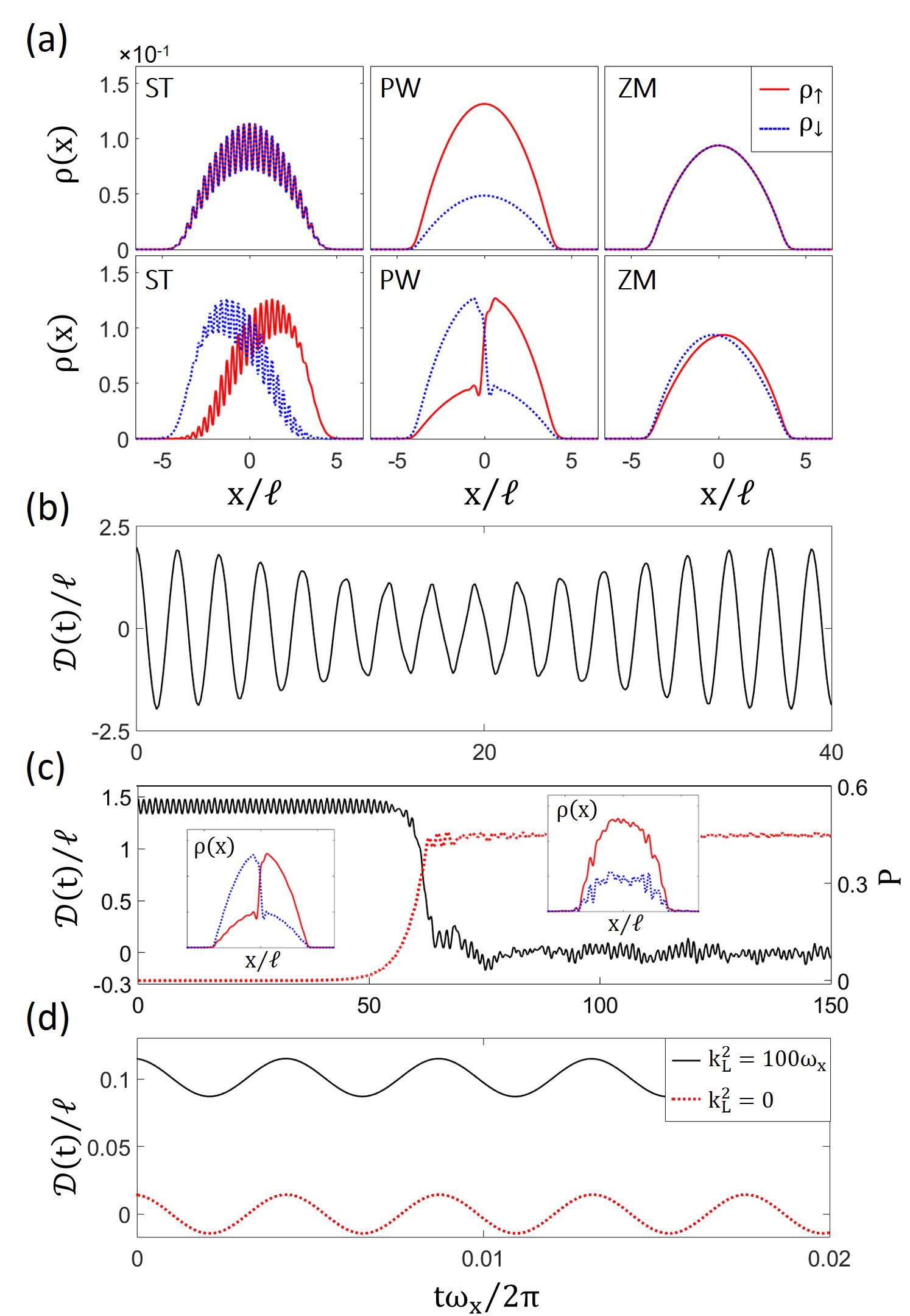
Fig. 2

This work has been published, see http://journals.aps.org/pra/abstract/10.1103/PhysRevA.95.033616.

Reference:

[1] N. Goldman, G. Juzeliunas, P. Ohberg, and I. B. Spielman, Rep. Prog. Phys. 77, 126401 (2014).

[2] H. Zhai, Rep. Prog. Phys. 78, 026001 (2015).

[3] Y.-J. Lin, K. Jimenez-Garcia, and I. B. Spielman, Nature (London). 471, 83 (2011).

[4] P. Wang, Z.-Q. Yu, Z. Fu, J. Miao, L. Huang, S. Chai, H. Zhai, and J. Zhang, Phys. Rev. Lett. 109, 095301 (2012).

[5] L. W. Cheuk, A. T. Sommer, Z. Hadzibabic, T. Yefsah, W. S. Bakr, and M. W. Zwierlein, Phys. Rev. Lett. 109, 095302 (2012).

[6] Y. Li, L. P. Pitaevskii, and S. Stringari, Phys. Rev. Lett. 108, 225301 (2012).

[7] S.-C. Ji, J.-Y. Zhang, L. Zhang, Z.-D. Du, W. Zheng, Y.-J. Deng, H. Zhai, S. Chen, and J.-W. Pan, Nature Phys. 10, 314 (2014).

[8] H. Hu, B. Ramachandhran, H. Pu, and X.-J. Liu, Phys. Rev. Lett. 108, 010402 (2012); S. Sinha, R. Nath, and L. Santos, Phys. Rev. Lett. 107, 270401 (2011).