Bethe-Ansatz专家管习文来我组作系列报告[2017-11-10]
Topological Phase Transition and Charge Pumping in a One-Dimensional Periodically Driven Optical Lattice[2017-07-30]
山西大学2017研究生毕业典礼[2017-06-25]
CAT小组刘彦霞同学通过博士学位论文答辩[2017-06-03]
王利CSC公派访学结束回所工作[2017-05-22]
尹相国回到冷原子理论研究组工作[2017-04-13]
Spectroscopy and spin dynamics for strongly interacting few spinor bosons in one-dimensional traps[2017-04-06]
Collective excitation of a trapped Bose-Einstein condensate with spin-orbit coupling [2017-03-16]
Quantum walks in the commensurate off-diagonal AAH model[2017-02-03]
刘娜获得2016硕士国家奖学金[2017-01-12]

发布者： admin 发布时间：2017-07-30

　　

The study of topological phases of matters has been an important subject in condensed matter physics. In recent years, great efforts have been made to realize topological quantum systems in some new physical systems, such as periodically driven optical lattices in cold atomic systems. People expect the time-periodic driving of parameters of the systems can realize a significantly change of the band structures of the effective Floquet Hamiltonian and provide an additional freedom to adjust nontrivially topological bands.

     

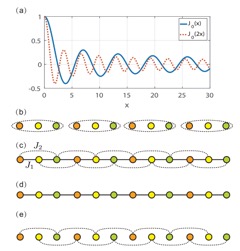
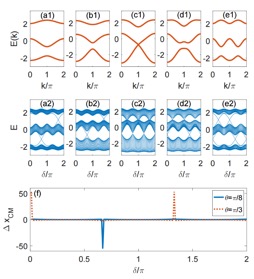
Fig. 1                                                                       Fig. 2

So far, the experimental efforts and almost all the theoretical works focused on only the nearest-neighbor (NN) hopping processes, due to the tunneling amplitudes between next-nearest-neighbor (NNN) sites decay very quickly and are generally negligible in comparison with the NN hopping term. In our latest work, we report a breakthrough in exhibitting topologically nontrivial phase transition in a one-dimensional (1D) periodically driving bichromatic optical lattice system which can be described by a superlattice model with adjustable NN and NNN hopping terms. In comparison with the 1D superlattice model described by the Harper model, the system provides different topological behaviors when the NNN hopping amplitude $J_2$ is larger than the NN one $J_1$ [see Fig.1]. By tuning the ratio of nearest-NN and NNN hopping amplitudes, the system undergoes a topological phase transition accompanied by the change of topological numbers, energy gap closing and nontrivial edge states [see Fig.2]. Particularly, recent progress in in situ detection with the single-site resolution offers the possibility of the detection of topological charge pumping. Using a slowly time-periodic modulation, the system emerges distinct quantized topological pumped charges of atoms in the filled band for different topological phases [see Fig. 3].

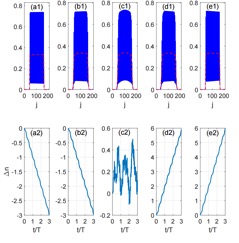
Fig. 3

The bichromatic optical lattices can be generated by superimposing two 1D optical lattices with different wavelengths, which has led to experimental observation of Anderson localization of a noninteracting BEC in 1D incommensurate optical lattices and Zak phase of Su-Schrieffer-Heeger model. By periodically driving shallow optical superlattices, we may expect that it is feasible to experimentally detect nontrivially topological phase transition induced by time-periodic driving discussed in the present work.

This work opens a path to the realization of new types of topological phase transition in 1D periodically driven superlattice systems. Our theory will provide new insights to understand topological phase transition.

This work has been published, see https://journals.aps.org/pra/abstract/10.1103/PhysRevA.96.013606